マリオの完コピvol.28 ジャンプの解析と修正
ジャンプの挙動と値を修正する事にした。
オリジナルのジャンプを1フレームずつ撮影し、その時のマリオの帽子の高さよりY座標を求め、それをエクセルに入力してグラフにしてみた。
すると新たな発見があった。Aボタン押しっぱなしの時とAボタンを途中で離した時でグラフの形が変わっていたのだ。
■Aボタンを押しっぱなしのグラフ
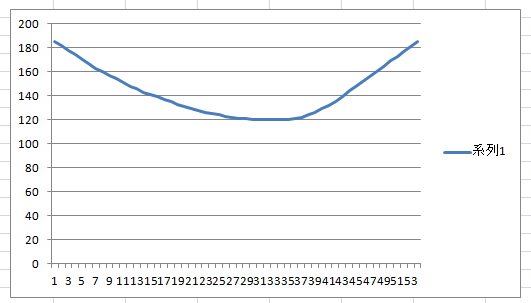
■Aボタンを途中で離した時のグラフ
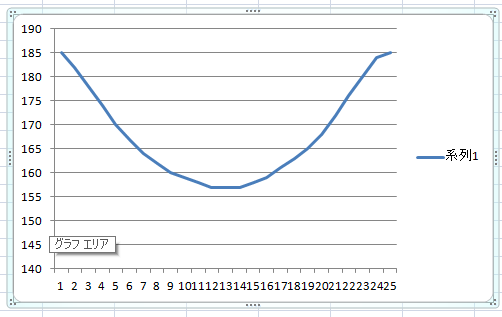
Aボタンを押しっぱなしのほうは、左右対称の放物線ではないので上昇時と落下時で加速度が違う事が分かる。
Aボタンを途中で離した時は、左右対称の放物線っぽく見えるが、値が少しずれているため、ボタンを離すまでは↑の上昇時と同じ加速度がかかり、離した時から違う加速度がかかっていると想像する。
また別に、ジャンプではなく落下時だけのデータも取得してグラフにしてみた。
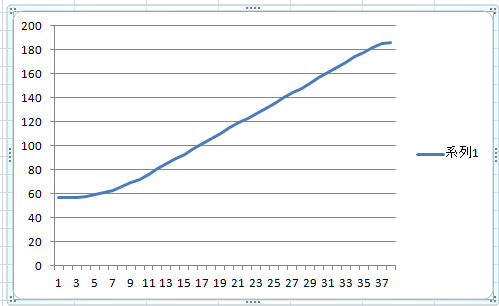
こちらは途中まで加速し、そこから一定速度になっている事が分かる。これにより落下の最大速度が設定されている事が分かる。
次にジャンプ上昇時の起点と終点の数値より、物理の方程式を使って加速度と初速を求めてみた。
Δx = v0 * t + 1/2 * a * t^2
v = v0 + a * t
この2つの式を使って連立方程式を解けばいける。
中3か高1くらいの分野と思うが、現役を離れて忘れていたので、この本を引っ張り出してみた。

そして計算した結果
加速度は-0.126953125ピクセル/フレーム^2
初速は4.0624ピクセル/フレーム
となった。
導いた式を使って実際の値を比べてみると、ほぼ一致していたので、等加速度運動になっている感じだ。
↓Aの列がオリジナルの値で、Iの列が計算結果の値
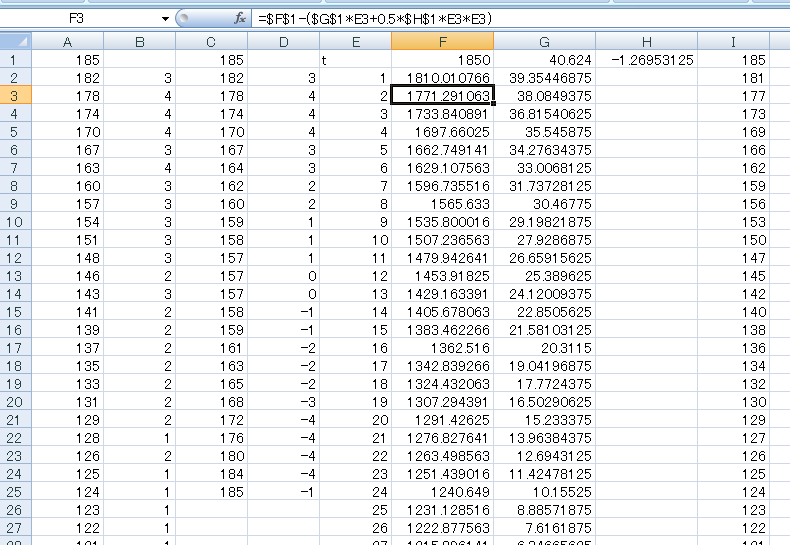
以上より仕様をまとめると
・上昇時と下降時で重力が違う。
・等加速度運動である。
・落下時は最大速度がある。
そこで以前に書いたジャンプ実装の記事が間違っていた事が分かる。
http://blog.game-kids.net/haruzakki/page-6.html
こちらの記事では、ジャンプで必要そうなパラメータは以下の4つを挙げていた。
1.ジャンプした瞬間の力
2.加速度(重力)
3.ボタンを押す時間の最大フレーム数
4.落下時の最大速度
このうち、2は細分化され、上昇時と下降時とで分かれる。
3は不要である。
次に、オリジナルの完コピを目指しているため、正確な値を入力してみたい。
で、風の噂でオリジナルの値を知る事が出来た。
まず、マリオの停止低速時、低速ダッシュ時、高速ダッシュ時の3パターンに分かれている。
低速時においては、上昇重力は0x20、下降重力は0x70、入力値は0xFC、抑制力は0x00であるようだ。
何のこっちゃよく分からないが、入力値の0xFCは10進数にすると252であり、256から引くと4となる。
上昇重力の0x20は10進数で32であり、その値を256で割ると0.125である。
この2つの数値は先ほど求めた
・初速は4.0624ピクセル/フレーム
・加速度は-0.126953125ピクセル/フレーム^2
の値に限りなく近い。
そしてこの値を使ってやってみた結果、ほぼオリジナルと同じ動きを再現する事ができた。
ダッシュジャンプの最高点の高さも一致している。

再現できた時には中々感動した。
ジャンプについてはいろいろググって調べてみたが、サンプルはどれもマリオのジャンプとは違っていた。
これとか
http://aidiary.hatenablog.com/entry/20050613/1255785116
これとか
http://d.hatena.ne.jp/Gemma/20080517/1211010942
http://www.geocities.jp/teruakigemma/jsmario/jsmario.html
2つ目の記事ではVerlet法というのを使ってやってて、この方法じゃないと出来ないのかと思ったけど、別に速度と加速度を使っても同じように出来るので騙されるところだった。
マリオのジャンプの肝は『上昇時と下降時で重力を分ける』。これに尽きる。
ボタン押し続けている間は上昇時の重力がかかるので、ボタンを押す時間によってジャンプ力が変わるというのも再現できるということだ。
重力が同じなら、ボタンを押し続けている間のフレーム数をカウントして、いろいろ処理しないといけない。
↑の最後のサンプルはそれに引っかかって5フレーム分のカウントをとるようにしていた。
物理法則には従わないこの方法を考えた人は天才だ。
初速と重力2つ。これでボタンを押す長さによって高さが変わるジャンプが再現できる。素晴らしい。
オリジナルのジャンプを1フレームずつ撮影し、その時のマリオの帽子の高さよりY座標を求め、それをエクセルに入力してグラフにしてみた。
すると新たな発見があった。Aボタン押しっぱなしの時とAボタンを途中で離した時でグラフの形が変わっていたのだ。
■Aボタンを押しっぱなしのグラフ

■Aボタンを途中で離した時のグラフ

Aボタンを押しっぱなしのほうは、左右対称の放物線ではないので上昇時と落下時で加速度が違う事が分かる。
Aボタンを途中で離した時は、左右対称の放物線っぽく見えるが、値が少しずれているため、ボタンを離すまでは↑の上昇時と同じ加速度がかかり、離した時から違う加速度がかかっていると想像する。
また別に、ジャンプではなく落下時だけのデータも取得してグラフにしてみた。

こちらは途中まで加速し、そこから一定速度になっている事が分かる。これにより落下の最大速度が設定されている事が分かる。
次にジャンプ上昇時の起点と終点の数値より、物理の方程式を使って加速度と初速を求めてみた。
Δx = v0 * t + 1/2 * a * t^2
v = v0 + a * t
この2つの式を使って連立方程式を解けばいける。
中3か高1くらいの分野と思うが、現役を離れて忘れていたので、この本を引っ張り出してみた。

そして計算した結果
加速度は-0.126953125ピクセル/フレーム^2
初速は4.0624ピクセル/フレーム
となった。
導いた式を使って実際の値を比べてみると、ほぼ一致していたので、等加速度運動になっている感じだ。
↓Aの列がオリジナルの値で、Iの列が計算結果の値

以上より仕様をまとめると
・上昇時と下降時で重力が違う。
・等加速度運動である。
・落下時は最大速度がある。
そこで以前に書いたジャンプ実装の記事が間違っていた事が分かる。
http://blog.game-kids.net/haruzakki/page-6.html
こちらの記事では、ジャンプで必要そうなパラメータは以下の4つを挙げていた。
1.ジャンプした瞬間の力
2.加速度(重力)
3.ボタンを押す時間の最大フレーム数
4.落下時の最大速度
このうち、2は細分化され、上昇時と下降時とで分かれる。
3は不要である。
次に、オリジナルの完コピを目指しているため、正確な値を入力してみたい。
で、風の噂でオリジナルの値を知る事が出来た。
まず、マリオの停止低速時、低速ダッシュ時、高速ダッシュ時の3パターンに分かれている。
低速時においては、上昇重力は0x20、下降重力は0x70、入力値は0xFC、抑制力は0x00であるようだ。
何のこっちゃよく分からないが、入力値の0xFCは10進数にすると252であり、256から引くと4となる。
上昇重力の0x20は10進数で32であり、その値を256で割ると0.125である。
この2つの数値は先ほど求めた
・初速は4.0624ピクセル/フレーム
・加速度は-0.126953125ピクセル/フレーム^2
の値に限りなく近い。
そしてこの値を使ってやってみた結果、ほぼオリジナルと同じ動きを再現する事ができた。
ダッシュジャンプの最高点の高さも一致している。

再現できた時には中々感動した。
ジャンプについてはいろいろググって調べてみたが、サンプルはどれもマリオのジャンプとは違っていた。
これとか
http://aidiary.hatenablog.com/entry/20050613/1255785116
これとか
http://d.hatena.ne.jp/Gemma/20080517/1211010942
http://www.geocities.jp/teruakigemma/jsmario/jsmario.html
2つ目の記事ではVerlet法というのを使ってやってて、この方法じゃないと出来ないのかと思ったけど、別に速度と加速度を使っても同じように出来るので騙されるところだった。
マリオのジャンプの肝は『上昇時と下降時で重力を分ける』。これに尽きる。
ボタン押し続けている間は上昇時の重力がかかるので、ボタンを押す時間によってジャンプ力が変わるというのも再現できるということだ。
重力が同じなら、ボタンを押し続けている間のフレーム数をカウントして、いろいろ処理しないといけない。
↑の最後のサンプルはそれに引っかかって5フレーム分のカウントをとるようにしていた。
物理法則には従わないこの方法を考えた人は天才だ。
初速と重力2つ。これでボタンを押す長さによって高さが変わるジャンプが再現できる。素晴らしい。